Newton's Method
Newton's Method
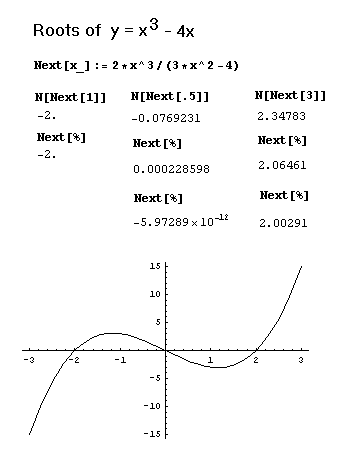
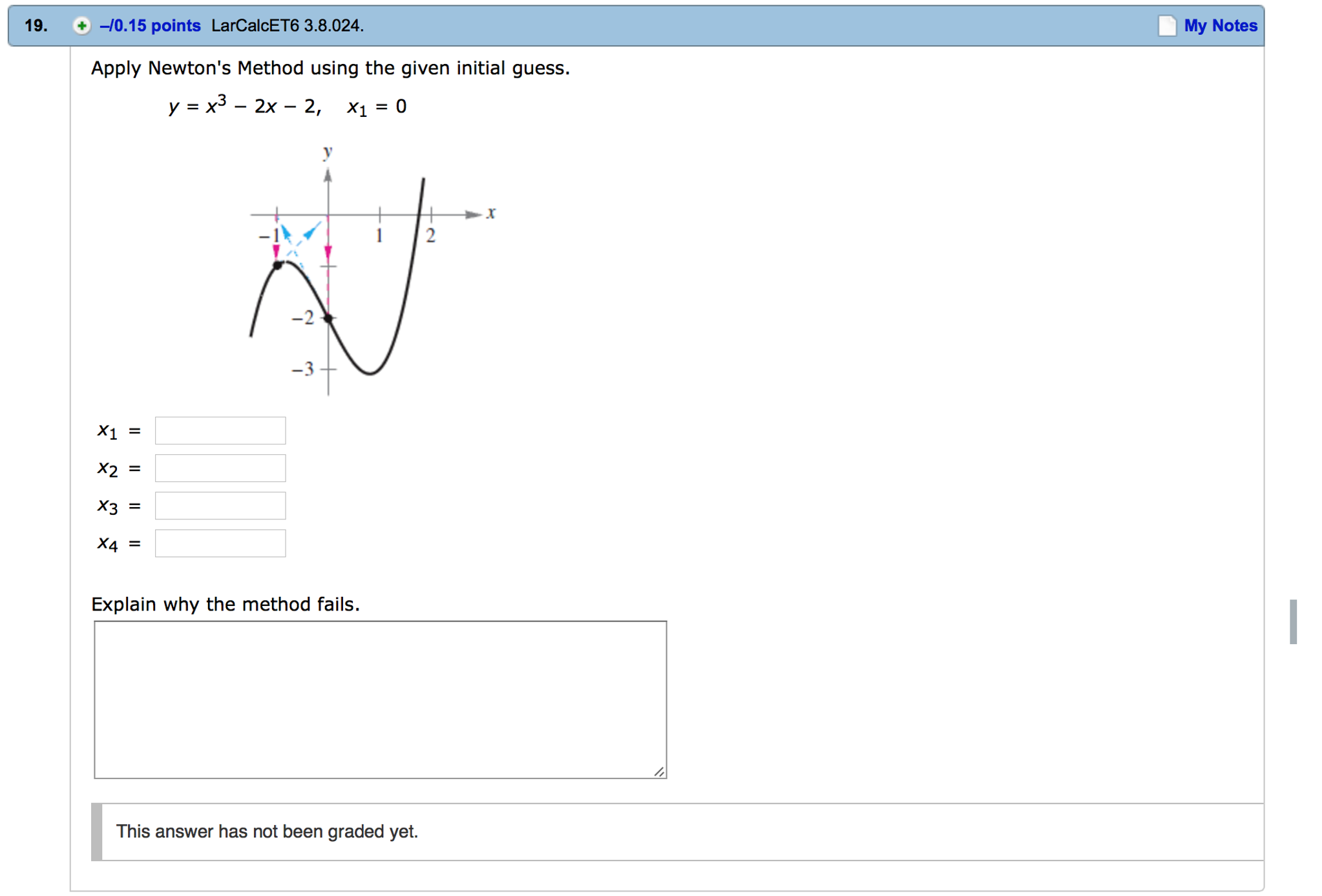
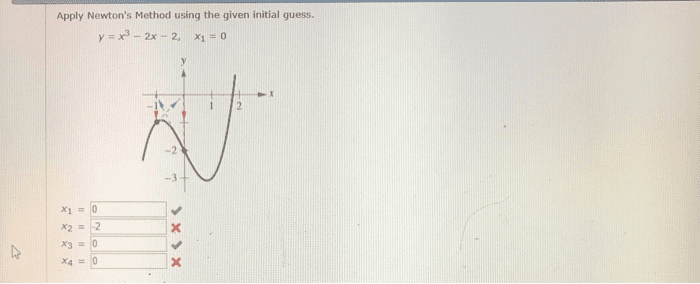
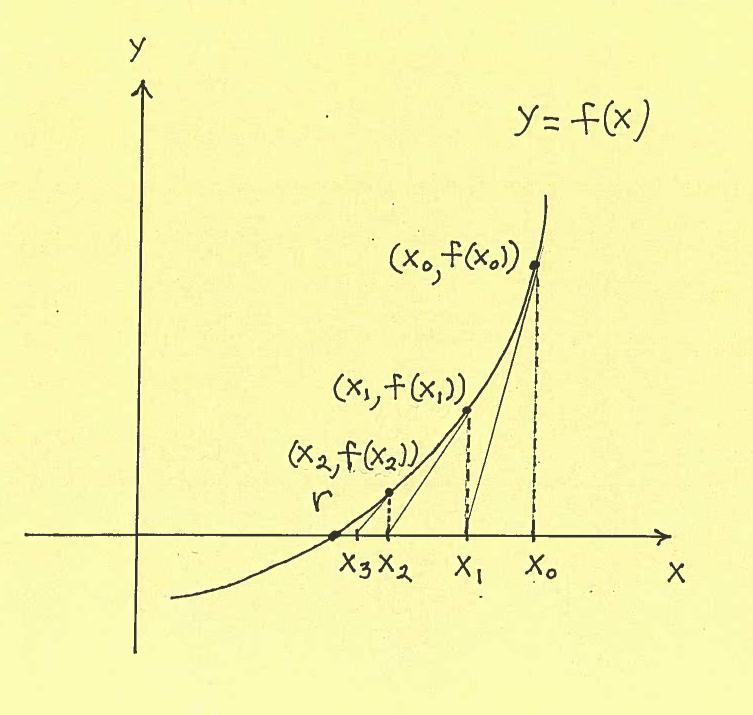
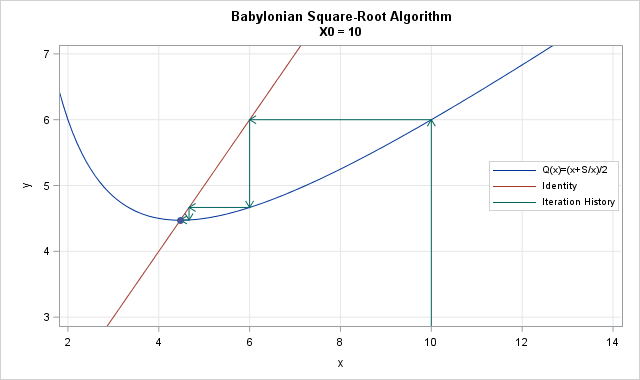
SOLVED: Use one iteration of Newton's Method with an initial guess of X1 2 to approximate the solution to cos(x) The approximation, xz equals 01 3t 113 0 DDtis not possible to compute x2
Content - Newton's method
The sensitivity of Newton's method to an initial guess - The DO Loop
Using the Newton-Raphson Method to find the Root of a Cubic Function - YouTube
Solved Apply Newton's Method using the given initial guess. | Chegg.com
Solved Apply Newton's Method using the given initial guess. | Chegg.com
OneClass: Apply Newton's Method using the given initial guess -2 x22 x3 = Show transcribed ima...
Solved 7. (a) Use Newton's method ONCE with an initial guess | Chegg.com
Solved Apply Newton's Method using the given initial guess. | Chegg.com
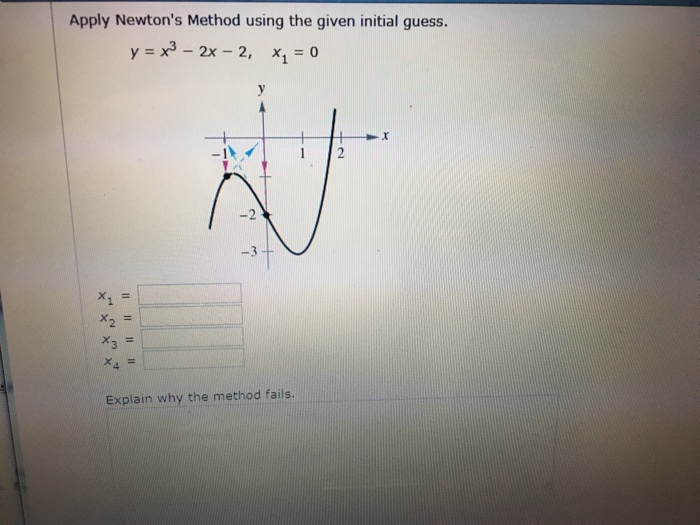
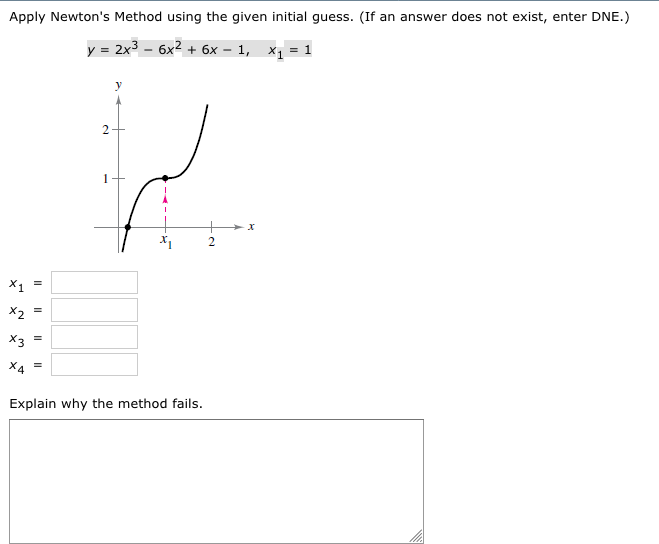
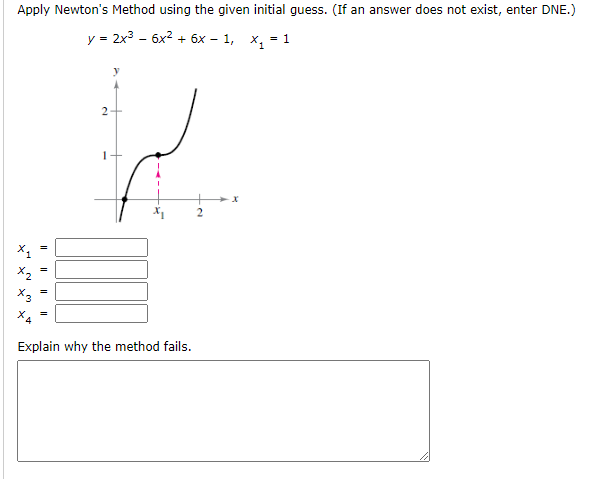
Apply Newton's Method using the given initial guess, and explain why the method fails. y= 2x^3 - 6x^2 + 6x -1 \ , \ x_1 = 1. (a) The method fails because
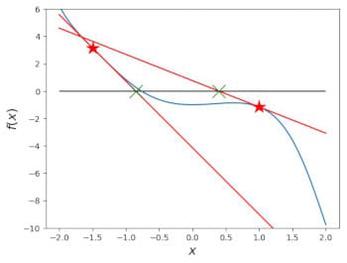
Given the following equation and initial guess, Newton's method fails to approximate a solution. (x - 2)^3 + 4, x_1 = 2 Why did Newton's method fail? Select one: a. The slopes
Answered: Use newton Raphson Method to find the… | bartleby
Newton raphson method for finding root | Class Twelve Maths
How to Find the Initial Guess in Newton's Method – ComputingSkillSet.com
The sensitivity of Newton's method to an initial guess - The DO Loop
Newton's Method
Apply Newton's Method using the given initial guess, and exp | Quizlet
All I really need to know about Newton's method I learned in primary school - The DO Loop
SOLVED: Newton's Method will fail to approximate the solution to f(w) = 0 with initial guess To when: f' (To) f(z) is not differentiable at €o: f(z) is not a polynomial. To
How to Find the Initial Guess in Newton's Method – ComputingSkillSet.com
Newton's Method
Solved Apply Newton's Method using the given initial guess. | Chegg.com
2. Newton's method (or Newton-Raphson method) is a | Chegg.com
